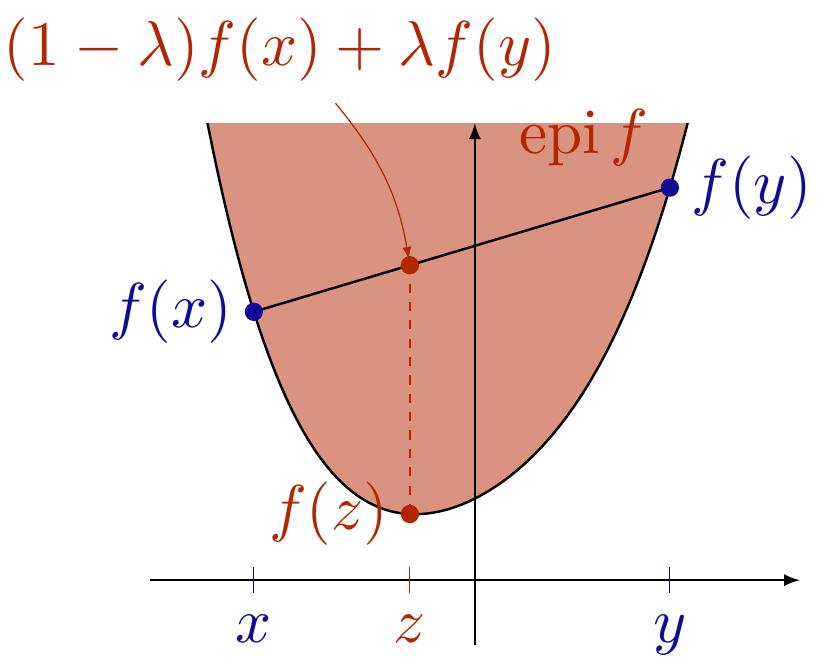
T. Rockafellar stated in a SIAM review: "The watershed in optimization is between convexity and non-convexity instead of linearity and non-linearity". For many decades linear optimization problems were considered as solvable and non-linear problems as very difficult to solve. However, the development of fundamental convex analysis tools such as Fenchel duality changed this picture. A broad and deep understanding of the theory led to many efficient algorithms for convex optimization problems, which has also contributed to the advance of applications, for example, in machine learning, computer vision, image processing, and compressed sensing.
The course introduces basic and advanced concepts of convex analysis. After definition, generation, and relations of convexity for sets and functions are studied, slightly more advanced tools such as the Moreau envelope, the subdifferential, and Fermat's rule are developed. These tools are fundamental for the study of convex optimization problems, optimality conditions, and algorithms. The second part of the lecture is devoted to the analysis of first order convex optimization algorithms that are ubiquitious in data science applications such as Image Processing, Computer Vision, Machine Learning and Statistics. Then, the study of convex duality allows us to introduce widely used primal-dual algorithms.
After taking the course, students know about the most relevant concepts of convex analysis and convex optimization. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of convex optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they develop basic skills in solving practical problems with Python.
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
Optimization methods or algorithms seek for a state of a system that is optimal with respect to an objective function. Depending on the properties of the objective function, different strategies may be used to find such an optimal state (or point). The fundamental knowledge of the classes of functions that can be optimized, the properties of available optimization strategies, and the properties of the optimal points are crucial for appropriately modeling practical real world problems as optimization problems. An exact model of the real world that cannot be solved is as useless as a too simplistic model that can be solved easily.
This lecture introduces the basic algorithms, and concepts and analysis tools for several fundamental classes of continuous optimization problems and algorithms. The lecture covers the basics of generic Descent Methods, Gradient Descent, Newton Method, Quasi-Newton Method, Gauss-Newton Method, Conjugate Gradient, linear programming, non-linear programming, as well as optimality conditions for unconstrained and constrained optimization problems. These may be considered as the classical topics of continuous optimization. Some of these methods will be implemented and explored for practical problems in the tutorials.
After taking this course, students will have an overview of classical optimization methods and analysis tools for continuous optimization problems, which allows them to model and solve practical problems. Moreover, in the tutorials, some experience will be gained to implement and numerically solve practical problems.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
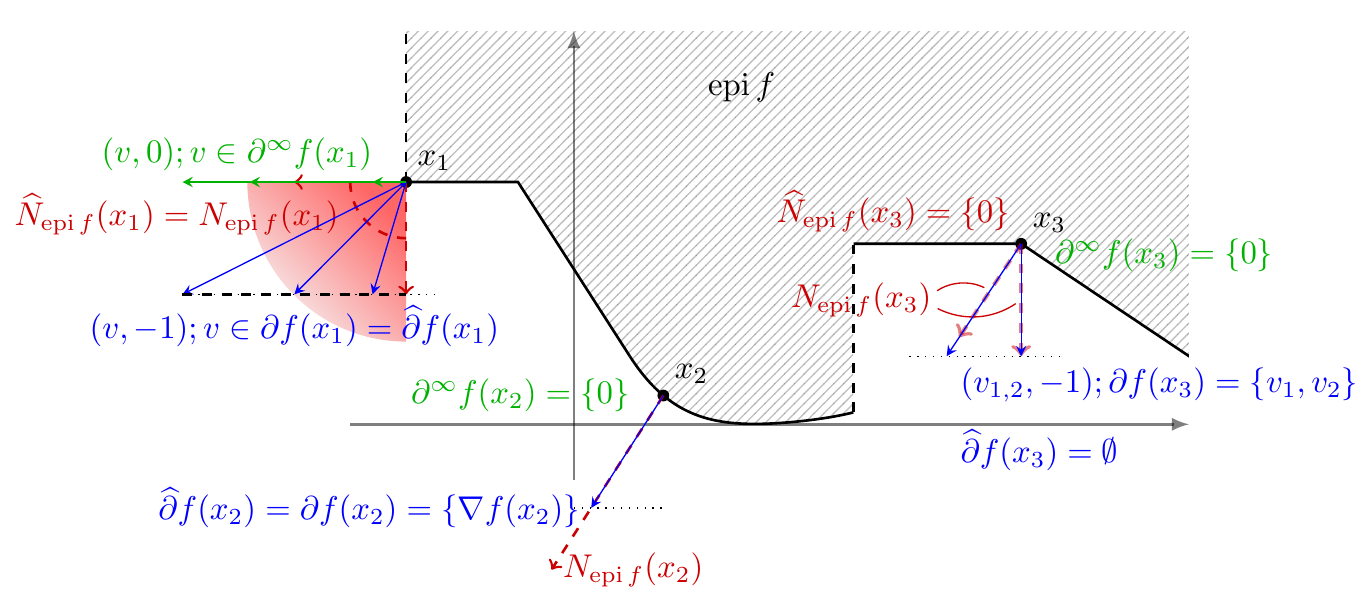
In many Data Science applications, non-smooth features arise naturally, e.g., in the analysis of sparsity, low rank structure, or low complexity regularization in general. Constrained optimization problems can be considered as non-smooth objective functions. Envelope functions, dual Lagrangian relaxations, and many other (algorithmically) important functions are naturally non-smooth. Thereby, non-smoothness is clearly not just an artifact, it is a feature that usually comes with a certain structure. The key is to recognize good structures that can be leveraged. Ignoring the non-smoothness leads to inaccurate solutions or slow algorithms.
The course consists of two parts: (1) basic and advanced concepts of non-smooth analysis and (2) optimization algorithms for non-smooth non-convex optimization that are widely used in non-convex optimization for data science (Machine Learning, Computer Vision, Image Processing, and Statistics, ...). The first milestone in Part 1 is the exploration of Fermat's Rule, a first order optimality condition for non-smooth functions. This requires us to introduce generalized derivatives and is a means to formulate commonly employed Lagrange multiplier rules or KKT conditions as a special case. In order to study algorithms in Part 2 to solve non-smooth non-convex optimization problems, we first introduce the class of semi-algebraic and tame functions that comprise all practically relevant functions, but exclude pathological function. This leads to insights into recent breakthroughs in non-smooth and non-convex optimization that yield strong convergence results to a stationary point, based on the so-called Kurdyka-Lojasiewicz inequality. Besides many classical applications, this lecture presents several research topics in optimization for machine learning, for example,
(i) the convergence of SGD, a popular stochastic gradient method, to stationary points,
(ii) the mathematical rigorous formulation of automatic differentiation programs such as implemented in PyTorch,
(iii) and bilevel optimization, which can be seen as a formalization of parameter learning problems.
After taking the course, students know about the most relevant concepts of non-smooth analysis and optimization, beyond convexity. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they are able to perform the convergence analysis for non-convex optimization algorithms and they develop basic skills in solving practical problems with Python.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
Optimization methods or algorithms seek for a state of a system that is optimal with respect to an objective function. Depending on the properties of the objective function, different strategies may be used to find such an optimal state (or point). The fundamental knowledge of the classes of functions that can be optimized, the properties of available optimization strategies, and the properties of the optimal points are crucial for appropriately modeling practical real world problems as optimization problems. An exact model of the real world that cannot be solved is as useless as a too simplistic model that can be solved easily.
This lecture introduces the basic algorithms, and concepts and analysis tools for several fundamental classes of continuous optimization problems and algorithms. The lecture covers the basics of generic Descent Methods, Gradient Descent, Newton Method, Quasi-Newton Method, Gauss-Newton Method, Conjugate Gradient, linear programming, non-linear programming, as well as optimality conditions for unconstrained and constrained optimization problems. These may be considered as the classical topics of continuous optimization. Some of these methods will be implemented and explored for practical problems in the tutorials.
After taking this course, students will have an overview of classical optimization methods and analysis tools for continuous optimization problems, which allows them to model and solve practical problems. Moreover, in the tutorials, some experience will be gained to implement and numerically solve practical problems.
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
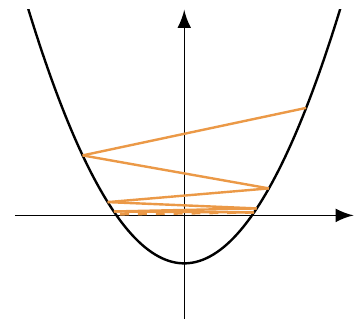
Optimization methods or algorithms seek for a state of a system that is optimal with respect to an objective function. Depending on the properties of the objective function, different strategies may be used to find such an optimal state (or point). The fundamental knowledge of the classes of functions that can be optimized, the properties of available optimization strategies, and the properties of the optimal points are crucial for appropriately modeling practical real world problems as optimization problems. An exact model of the real world that cannot be solved is as useless as a too simplistic model that can be solved easily.
This lecture introduces the basic algorithms, and concepts and analysis tools for several fundamental classes of continuous optimization problems and algorithms. The lecture covers the basics of generic Descent Methods, Gradient Descent, Newton Method, Quasi-Newton Method, Gauss-Newton Method, Conjugate Gradient, linear programming, non-linear programming, as well as optimality conditions for unconstrained and constrained optimization problems. These may be considered as the classical topics of continuous optimization. Some of these methods will be implemented and explored for practical problems in the tutorials.
After taking this course, students will have an overview of classical optimization methods and analysis tools for continuous optimization problems, which allows them to model and solve practical problems. Moreover, in the tutorials, some experience will be gained to implement and numerically solve practical problems.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
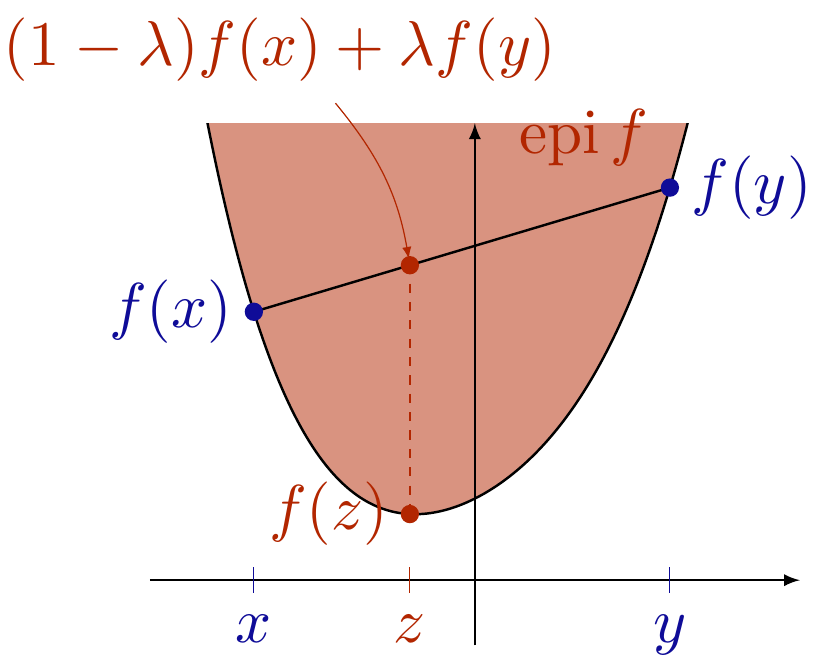
T. Rockafellar stated in a SIAM review: "The watershed in optimization is between convexity and non-convexity instead of linearity and non-linearity". For many decades linear optimization problems were considered as solvable and non-linear problems as very difficult to solve. However, the development of fundamental convex analysis tools such as Fenchel duality changed this picture. A broad and deep understanding of the theory led to many efficient algorithms for convex optimization problems, which has also contributed to the advance of applications, for example, in machine learning, computer vision, image processing, and compressed sensing.
The course introduces basic and advanced concepts of convex analysis. After definition, generation, and relations of convexity for sets and functions are studied, slightly more advanced tools such as the Moreau envelope, the subdifferential, and Fermat's rule are developed. These tools are fundamental for the study of convex optimization problems, optimality conditions, and algorithms. The second part of the lecture is devoted to the analysis of first order convex optimization algorithms that are ubiquitious in data science applications such as Image Processing, Computer Vision, Machine Learning and Statistics. Then, the study of convex duality allows us to introduce widely used primal-dual algorithms.
After taking the course, students know about the most relevant concepts of convex analysis and convex optimization. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of convex optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they develop basic skills in solving practical problems with Python.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
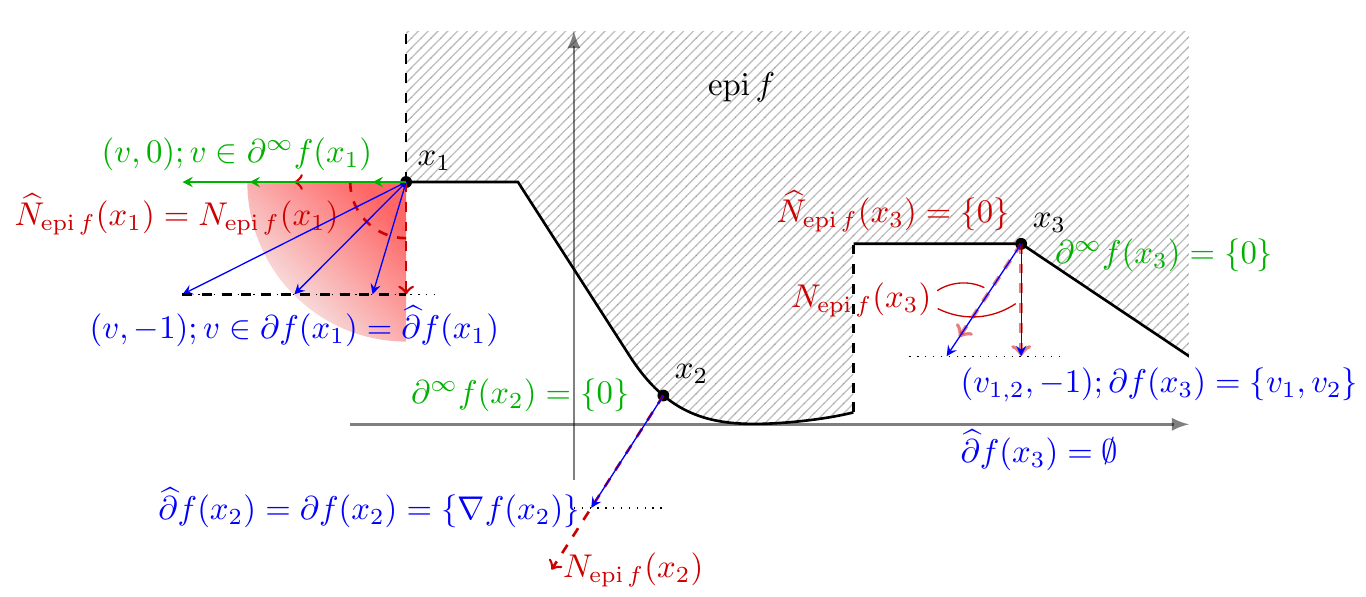
In many Data Science applications, non-smooth features arise naturally, e.g., in the analysis of sparsity, low rank structure, or low complexity regularization in general. Constrained optimization problems can be considered as non-smooth objective functions. Envelope functions, dual Lagrangian relaxations, and many other (algorithmically) important functions are naturally non-smooth. Thereby, non-smoothness is clearly not just an artifact, it is a feature that usually comes with a certain structure. The key is to recognize good structures that can be leveraged. Ignoring the non-smoothness leads to inaccurate solutions or slow algorithms.
The course consists of two parts: (1) basic and advanced concepts of non-smooth analysis and (2) optimization algorithms for non-smooth non-convex optimization that are widely used in non-convex optimization for data science (Machine Learning, Computer Vision, Image Processing, and Statistics, ...). The first milestone in Part 1 is the exploration of Fermat's Rule, a first order optimality condition for non-smooth functions. This requires us to introduce generalized derivatives and is a means to formulate commonly employed Lagrange multiplier rules or KKT conditions as a special case. In order to study algorithms in Part 2 to solve non-smooth non-convex optimization problems, we first introduce the class of semi-algebraic and tame functions that comprise all practically relevant functions, but exclude pathological function. This leads to insights into recent breakthroughs in non-smooth and non-convex optimization that yield strong convergence results to a stationary point, based on the so-called Kurdyka-Lojasiewicz inequality. Besides many classical applications, this lecture presents several research topics in optimization for machine learning, for example,
(i) the convergence of SGD, a popular stochastic gradient method, to stationary points,
(ii) the mathematical rigorous formulation of automatic differentiation programs such as implemented in PyTorch,
(iii) and bilevel optimization, which can be seen as a formalization of parameter learning problems.
After taking the course, students know about the most relevant concepts of non-smooth analysis and optimization, beyond convexity. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they are able to perform the convergence analysis for non-convex optimization algorithms and they develop basic skills in solving practical problems with Python.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
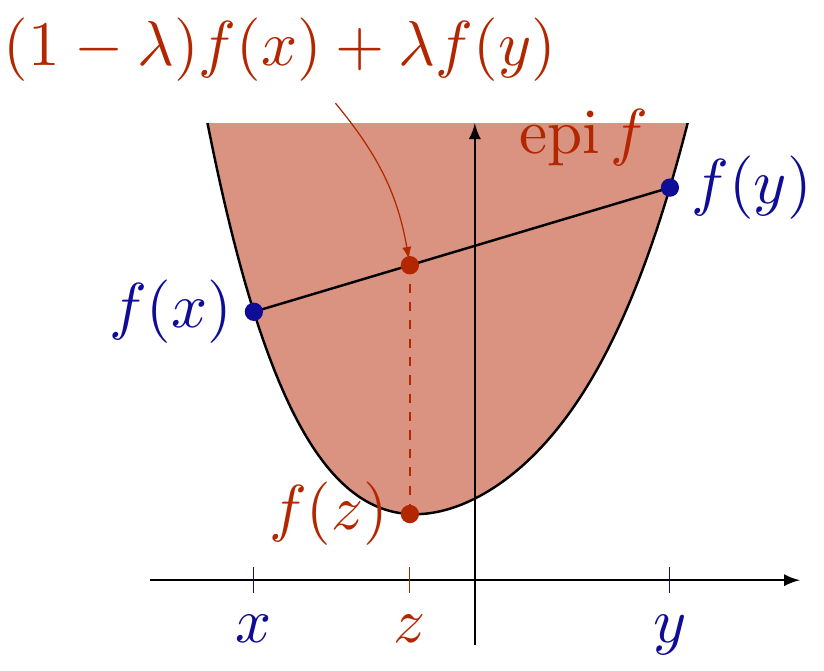
T. Rockafellar stated in a SIAM review: "The watershed in optimization is between convexity and non-convexity instead of linearity and non-linearity". For many decades linear optimization problems were considered as solvable and non-linear problems as very difficult to solve. However, the development of fundamental convex analysis tools such as Fenchel duality changed this picture. A broad and deep understanding of the theory led to many efficient algorithms for convex optimization problems, which has also contributed to the advance of applications, for example, in machine learning, computer vision, image processing, and compressed sensing.
The course introduces basic and advanced concepts of convex analysis. After definition, generation, and relations of convexity for sets and functions are studied, slightly more advanced tools such as the Moreau envelope, the subdifferential, and Fermat's rule are developed. These tools are fundamental for the study of convex optimization problems, optimality conditions, and algorithms. The second part of the lecture is devoted to the analysis of first order convex optimization algorithms that are ubiquitious in data science applications such as Image Processing, Computer Vision, Machine Learning and Statistics. Then, the study of convex duality allows us to introduce widely used primal-dual algorithms.
After taking the course, students know about the most relevant concepts of convex analysis and convex optimization. They are able to read and understand related scientific literature. Moreover, they can rate the difficulty of convex optimization problems arising in applications in machine learning or computer vision and select an efficient algorithm accordingly. Moreover, they develop basic skills in solving practical problems with Python.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
Optimization methods or algorithms seek for a state of a system that is optimal with respect to an objective function. Depending on the properties of the objective function, different strategies may be used to find such an optimal state (or point). The fundamental knowledge of the classes of functions that can be optimized, the properties of available optimization strategies, and the properties of the optimal points are crucial for appropriately modeling practical real world problems as optimization problems. An exact model of the real world that cannot be solved is as useless as a too simplistic model that can be solved easily.
This lecture introduces the basic algorithms, and concepts and analysis tools for several fundamental classes of continuous optimization problems and algorithms. The lecture covers the basics of generic Descent Methods, Gradient Descent, Newton Method, Quasi-Newton Method, Gauss-Newton Method, Conjugate Gradient, linear programming, non-linear programming, as well as optimality conditions for unconstrained and constrained optimization problems. These may be considered as the classical topics of continuous optimization. Some of these methods will be implemented and explored for practical problems in the tutorials.
After taking this course, students will have an overview of classical optimization methods and analysis tools for continuous optimization problems, which allows them to model and solve practical problems. Moreover, in the tutorials, some experience will be gained to implement and numerically solve practical problems.
- DozentIn: Tejas Natu
- DozentIn: Peter Ochs
- DozentIn: Shida Wang
