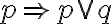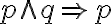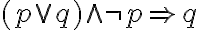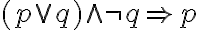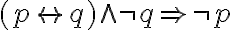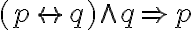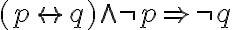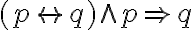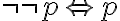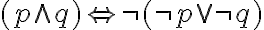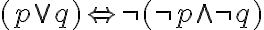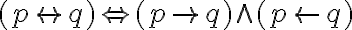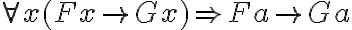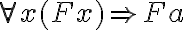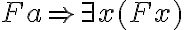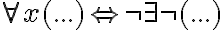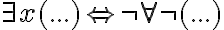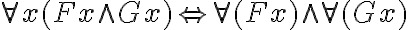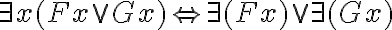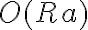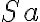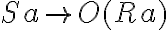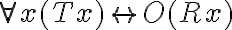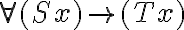Logische Folgerungsbeziehung
Deduktive Gültigkeit
Die logische Folgerungsbeziehung in der modernen Logik
Prof. Dr. Dr. h.c. Helmut Rüßmann
Über Folgerungsbeziehungen denkt man schon seit mehreren tausend Jahren nach. Der erste uns bekannte große Wurf war die aristotelische Syllogistik. Sie erfasst aber nur einen Teilbereich der logisch gültigen Schlussverfahren aus dem Bereich der Prädikatenlogik erster Stufe.
Eine präzise Bestimmung der logischen Folgerungsbeziehung zwischen Sätzen verdanken wir der modernen Logik, deren Entwicklungen etwa gegen Ende des 19. Jahrhunderts einsetzen. Man muss aber auch schon früher über die Syllogistik des Aristoteles hinaus gegangen sein. Denken wir etwa an Namen wie modus ponendo ponens oder modus tollendo tollens und rufen uns den berühmt berüchtigten Satz "Wenn es regnet, ist die Straße nass", "Es regnet", "Also ist die Straße nass" in Erinnerung, so treffen wir auf Folgerungsbeziehungen (modi), die sich mit den Regeln der Syllogistik nicht darstellen lassen, weil sie nicht aus kategorischen Urteilen gebildet sind. Aber schon die Scholastiker kannten diese Schlussformen.
| 1. | modus ponendo ponens |
|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. |
| Untersatz | Es regnet. |
| Schlusssatz | Die Straße ist nass. |
| 2. | modus tollendo tollens |
|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. |
| Untersatz | Die Straße ist nicht nass. |
| Schlusssatz | Es regnet nicht. |
| 3. | modus ??? |
|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. |
| Untersatz | Es regnet nicht. |
| Schlusssatz | Die Straße ist ???. |
Wir müssen nach anderen Wegen suchen, um uns des zwingenden Charakters solcher Schlüsse zu vergewissern. Die moderne Logik hat solche Wege gefunden. Sie zeichnet zunächst die logisch wahren Sätze als die Sätze aus, über deren Wahrheit allein auf Grund der in ihnen vorkommenden logischen Zeichen entschieden werden kann. Logische Zeichen sind Ausdrücke wie "nicht", "und", "oder", "wenn ..., dann ...", "alle", "einige", außerlogische Zeichen sind Individuennamen, Objektkonstanten und Prädikate. Die außerlogischen Zeichen beziehen sich auf Dinge dieser Welt. Den logischen Zeichen fehlt dieser Bezug. Sie bezeichnen nichts.
In der Logik arbeitet man mit Sätzen, die wahrheitsfähig sind. Diesen Begriff darf man weit verstehen und auf alle Sätze anwenden, über deren Richtigkeit und Geltung man sinnvoll streiten kann. In diesem Sinne wahrheitsfähige Sätze ohne logische Zeichen sind allein die sog. Atomsätze, in denen einem Individuum oder einem Objekt ein einstelliges Prädikat oder mehreren Objekten ein entsprechendes mehrstelliges Prädikat zugeschrieben wird. Alle anderen wahrheitsfähigen Sätze verwenden neben den außerlogischen Zeichen auch logische Zeichen.
Über die Gültigkeit eines Teils dieser Sätze kann nun allein auf Grund der Bedeutung der in ihnen vorkommenden logischen Zeichen befunden werden, was nichts anderes heißt als, dass die in ihnen auch vorkommenden außerlogischen Zeichen unwesentlich vorkommen und ohne Beinträchtigung des Wahrheitsgehalts des Satzes durch beliebige andere ersetzt werden können. So verhält es sich etwa mit dem Satz: "Julia ist blond, oder Julia ist nicht blond." Seine Gültigkeit braucht nicht durch eine empirische Untersuchung von Julias Haarfarbe bewiesen zu werden. Er ist wahr auf Grund der in ihm vorkommenden logischen Zeichen "oder" und "nicht", und Julia ist in ihm ebenso unwesentlich wie ihre Haarfarbe. Letzteres gilt auch bei umgekehrter Determination: der logischen Falschheit. Über den Satz: "Julia ist blond, und Julia ist nicht blond", können wir wiederum ohne Augenscheinsnahme befinden. Die Bedeutung der logischen Zeichen "und" und "nicht" schließen seine Gültigkeit a priori (vor jeder Erfahrung) aus.
Die logische Folgerungsbeziehung besteht nun zwischen solchen Sätzen, die in eine Wenn-dann-Verknüpfung gebracht einen logisch wahren Satz ergeben. Die Folgerungsbeziehung schließt es aus, dass der gefolgerte Satz, die Konklusion, falsch ist, während der Satz, aus dem er folgt, die Prämisse[n], wahr ist [sind]. Man beachte die mehrdeutige Verwendung von "wahr"! Logisch wahr ist die komplexe Wenn-dann-Verknüpfung. Deren Teilsätze, das Antecedens und das Konsequens, können zwar auch, müssen aber nicht logisch determiniert sein. In der Regel sind sie es nicht. Dann beurteilt sich ihre Wahrheit nach außerlogischen Kriterien (Korrespondenz, Konsens, Kohärenz). Es gibt demnach logisch wahre und falsche (analytische) Sätze und inhaltlich wahre und falsche (synthetische) Sätze. Zwischen ihnen vermittelt die Folgerungsbeziehung. Sie nämlich überträgt die (inhaltliche) Wahrheit der Prämisse[n] auf den gefolgerten Satz und die (inhaltliche) Falschheit des gefolgerten Satzes auf die Prämisse[n].
Nichtsdestoweniger handelt es sich bei der Folgerungsbeziehung selbst um eine rein formale Beziehung. Deshalb bietet sich, will man die bei komplexen Zusammenhängen immer gegebene Gefahr der Täuschung durch inhaltliche Erwägungen vermeiden, zu ihrer Überprüfung das formale und unbestechliche Instrumentarium der modernen Logik an. In ihr sind nicht zuletzt im Hinblick auf die inhaltlichen Funktionen formaler Operationen die Bedeutungen der logischen Zeichen eindeutig festgelegt.
Aussagen- oder Junktorenlogik
Da sind zunächst die oben angeführten (aussagen-)logischen Zeichen (Junktoren). Sie treten im Zusammenhang mit Sätzen auf, für die wir abkürzend “p, q, r ...” notieren, und sind in ihrer Bedeutung durch die Wahrheitswerte der Teilsätze des komplexen Satzes bestimmt. Man bringt dies in der Regel durch Wahrheitswerttabellen zum Ausdruck, kann es aber auch umgangssprachlich formulieren:
- ein mit
 negierter Satz ist dann wahr, wenn der Satz ohne
negierter Satz ist dann wahr, wenn der Satz ohne  falsch ist und umgekehrt (Negation);
falsch ist und umgekehrt (Negation); - ein mit
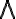 gebildeter komplexer Satz ist nur dann wahr, wenn die so verbundenen Teilsätze wahr sind; in allen anderen Fällen ist er falsch (Konjunktion);
gebildeter komplexer Satz ist nur dann wahr, wenn die so verbundenen Teilsätze wahr sind; in allen anderen Fällen ist er falsch (Konjunktion); - ein mit
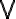 gebildeter komplexer Satz ist nur dann falsch, wenn sämtliche so verbundenen Teilsätze falsch sind; in allen anderen Fällen ist er wahr (Adjunktion, Disjunktion, Alternation);
gebildeter komplexer Satz ist nur dann falsch, wenn sämtliche so verbundenen Teilsätze falsch sind; in allen anderen Fällen ist er wahr (Adjunktion, Disjunktion, Alternation); - ein mit
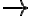 gebildeter komplexer Satz ist nur dann falsch, wenn der das Vorderglied (Antecedens) bildende Teilsatz wahr und der das Hinterglied (Konsequens) bildende Teilsatz falsch sind; in allen anderen Fällen ist er wahr (Konditional, materiale Implikation);
gebildeter komplexer Satz ist nur dann falsch, wenn der das Vorderglied (Antecedens) bildende Teilsatz wahr und der das Hinterglied (Konsequens) bildende Teilsatz falsch sind; in allen anderen Fällen ist er wahr (Konditional, materiale Implikation); - ein mit
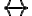 gebildeter komplexer Satz ist wahr, wenn die so verbundenen Teilsätze entweder beide wahr oder beide falsch sind; in den anderen Fällen ist er falsch (Bikonditional, Äquivalenz).
gebildeter komplexer Satz ist wahr, wenn die so verbundenen Teilsätze entweder beide wahr oder beide falsch sind; in den anderen Fällen ist er falsch (Bikonditional, Äquivalenz).
Die Definition aussagenlogischer Zeichen (Junktoren) durch Wahrheitswertverteilungen
| p | q | l-wahr | Alternation | Replikation | p | Konditional | q | Äquivalenz | Konjunktion | Exklusion | Kontravalenz | Nicht-q | Nicht-p | l-falsch | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w | w | w | w | w | w | w | w | w | w | f | f | f | f | f | f | f | f |
| w | f | w | w | w | w | f | f | f | f | w | w | w | w | f | f | f | f |
| f | w | w | w | f | f | w | w | f | f | w | w | f | f | w | w | f | f |
| f | f | w | f | w | f | w | f | w | f | w | f | w | f | f | w | w | f |
| A | B | Allmenge | Vereinigung | Einschluss | A | Einschluss | B | Identität | Durchschnitt | Nicht-B | Nicht-A | Nullmenge |
16 mögliche Kombinationen von Wahrheitswerten und deren Entsprechung in Sätzen und Satzkombinationen.
Die Kombinationen entsprechen den 16 möglichen Kombinationen von Mengen in der Mengenlehre. Wir konzentrieren uns auf die durch Junktoren bestimmte Aussagenlogik.
In den ersten beiden (blau unterlegten) Spalten links finden wir die vier möglichen Weltzustände der Kombination von Wahr- und Falschausagen zu p und q. Die weiteren Spalten zeigen uns die 16 möglichen Kombinationen der Wahrheitswertverteilungen in einem Viererfeld. Manche dieser Wahrheitswertverteilungen haben Namen. Einige stehen für umgangssprachliche Ausdrücke wie "und" (Konjunktion), "oder" (Alternation), "immer wenn ..., dann ..." (Konditional, hinreichende Bedingung), "nur wenn ..., dann ..." (Replikation, notwendige Bedingung), "genau wenn ..., dann ..." (Äquivalenz, hinreichende und notwendige Bedingung).
Jeder auch noch so komplexe aussagenlogische Ausdruck - jede auch noch so komplexe Kombination von Mengen - kann in einer endlichen Anzahl von Schritten ausgewertet werden. Die Auswertung gibt uns Auskunft über die Frage, ob der Satz (in seiner Geltung) logisch determiniert ist oder nicht.
- Logisch determiniert ist ein Satz, wenn über seine Wahrheit oder Falschheit allein mit logischen Mitteln entschieden werden kann.
- Ein Satz ist logisch wahr, wenn er wegen der Bedeutung der logischen Zeichen bei allen denkbaren Wahrheitswertverteilungen seiner Teilsätze - und damit in allen möglichen Welten - wahr ist.
- Ein Satz ist logisch falsch, wenn er wegen der Bedeutung der logischen Zeichen bei allen denkbaren Wahrheitswertverteilungen seiner Teilsätze - und damit in allen möglichen Welten - falsch ist.
- Ein Satz, der weder logisch wahr noch logisch falsch ist, heißt erfüllbar. Über sein Zutreffen kann nur mit außerlogischen Mitteln entschieden werden.
Eine Argumentation ist deduktiv gültig, wenn das Konditional mit den konjunktiv verbunden Gründen als Antecedens und der Konklusion als Konsequens logisch wahr ist.
Betrachten wir unter diesem Gesichtspunkt die Beispiele mit dem Regen und der Straße! "p" steht für "Es regnet", "q" für "Die Straße ist nass."
Wenn der Schluss
| 1. | modus ponendo ponens | symbolisiert |
|---|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. | 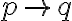 |
| Untersatz | Es regnet. | p |
| Schlusssatz | Die Straße ist nass. | q |
richtig sein soll, muss der Satz
logisch wahr sein, d.h. in allen möglichen Welten (Wahrheitswertkombinationen für p und q) wahr sein. Und so verhält es sich auch, weil es keinen Weltzustand gibt, in dem q falsch und beide Prämissen p und 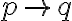 zugleich wahr wären.
zugleich wahr wären.
| p | q | ![{[(p}\rightarrow{q)}\wedge{p]}\rightarrow{q} {[(p}\rightarrow{q)}\wedge{p]}\rightarrow{q}](https://moodle.uni-saarland.de/filter/tex/pix.php/aa33347618c7078cdde6e309ed319dcf.gif) |
|---|---|---|
| w | w | w |
| w | f | w |
| f | w | w |
| f | f | w |
Falsch ist q nur in den Weltzuständen 2 und 4. Beim Zustand 4 ist aber auch p falsch. Beim Zustand 2 ist p zwar wahr; aber bei wahrem p und falschen q ist 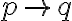 falsch.
falsch.
Wenn der Schluss
| 1. | modus tollendo tollens | symbolisiert |
|---|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. | 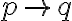 |
| Untersatz | Die Straße ist nicht nass. | 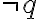 |
| Schlusssatz | Es regnet nicht. | 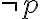 |
richtig sein soll, muss der Satz
logisch wahr sein, d.h. in allen möglichen Welten (Wahrheitswertkombinationen für p und q) wahr sein. Und so verhält es sich auch, weil es keinen Weltzustand gibt, in dem 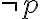 falsch und beide Prämissen
falsch und beide Prämissen 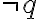 und zugleich
und zugleich 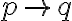 wahr wären.
wahr wären.
| p | q | ![{[(p}\rightarrow{q)}\wedge\neg{q]}\rightarrow\neg{p} {[(p}\rightarrow{q)}\wedge\neg{q]}\rightarrow\neg{p}](https://moodle.uni-saarland.de/filter/tex/pix.php/d535b045a96e3f3b87bdbff61e1f6352.gif) |
|---|---|---|
| w | w | w |
| w | f | w |
| f | w | w |
| f | f | w |
Falsch ist 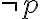 nur in den Weltzuständen 1 und 2. Beim Zustand 1 ist aber auch
nur in den Weltzuständen 1 und 2. Beim Zustand 1 ist aber auch 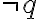 falsch. Beim Zustand 2 ist
falsch. Beim Zustand 2 ist 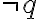 zwar wahr; aber bei wahrem p und falschen q ist
zwar wahr; aber bei wahrem p und falschen q ist 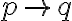 falsch.
falsch.
Wenn der Schluss
| 1. | modus ??? | symbolisiert |
|---|---|---|
| Obersatz | Wenn es regnet, ist die Straße nass. | 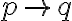 |
| Untersatz | Es regnet nicht. | 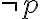 |
| Schlusssatz | Die Straße ist nicht nass. | 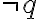 |
richtig sein soll, muss der Satz
logisch wahr sein, d.h. in allen möglichen Welten (Wahrheitswertkombinationen für p und q) wahr sein. Und so verhält es sich nicht, weil es einen Weltzustand gibt, in dem 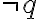 falsch und beide Prämissen
falsch und beide Prämissen 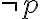 und
und 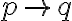 zugleich wahr sind.
zugleich wahr sind.
| p | q | ![{[(p}\rightarrow{q)}\wedge\neg{p]}\rightarrow\neg{q} {[(p}\rightarrow{q)}\wedge\neg{p]}\rightarrow\neg{q}](https://moodle.uni-saarland.de/filter/tex/pix.php/e43893859feec44da9db2622a49f6b23.gif) |
|---|---|---|
| w | w | w |
| w | f | w |
| f | w | f |
| f | f | w |
Falsch ist 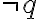 in den Weltzuständen 1 und 3. Beim Zustand 1 ist auch
in den Weltzuständen 1 und 3. Beim Zustand 1 ist auch 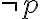 falsch. Beim Zustand 3 ist
falsch. Beim Zustand 3 ist 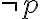 wahr und bei falschem p auch
wahr und bei falschem p auch 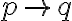 . Das macht den Gesamtausdruck falsch und erweist den Schluss als ungültig.
. Das macht den Gesamtausdruck falsch und erweist den Schluss als ungültig.
Aussagenlogisch gültige Schlussformen
Wir haben gelernt, wie man überprüfen kann, ob ein Schluss aussagenlogisch gültig ist. Im Folgenden wollen wir einfach einige bekannte aussagenlogisch gültige Schlussformen zusammenstellen. Dabei führen wir mit 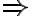 ein neues Zeichen für die logisch gültige Schlussform ein und notieren:
ein neues Zeichen für die logisch gültige Schlussform ein und notieren:
Zur Übung mag der Leser die Gültigkeit anhand der Wahrheitswertauswertung überprüfen. Das Konditional muss sich als logisch wahr erweisen.
Eine Steigerung der logischen Folgerungsbeziehung ist die logische Äquivalenz. Sie ist dadurch gekennzeichnet, dass die Folgerungsbeziehung nach beiden Richtungen besteht. Das können wir mit einem Doppelpfeil 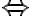 notieren und kommen zu den folgenden logischen Äquivalenzen aus dem Bereich der Aussagenlogik:
notieren und kommen zu den folgenden logischen Äquivalenzen aus dem Bereich der Aussagenlogik:
Steigerung der Variablenzahl
Der Vollständigkeit halber möchte ich nicht unerwähnt lassen, dass aussagenlogische Auswertungen selbstverständlich nicht auf Sätze mit zwei Satz- oder Aussagenvariablen beschränkt sind. Die Anzahl der in den Sätzen vorkommenden Variablen kann nahezu beliebig gesteigert werden. Mit der Steigerung erhöhen sich natürlich auch die möglichen Weltzustände. Bei zwei Variablen sind es vier mögliche Weltzustände, bei drei schon acht:
| p | q | r | ![[({p}\rightarrow{q})\wedge{(q}\rightarrow{r})]\rightarrow{(p\rightarrow{r})} [({p}\rightarrow{q})\wedge{(q}\rightarrow{r})]\rightarrow{(p\rightarrow{r})}](https://moodle.uni-saarland.de/filter/tex/pix.php/2fd83da1b55a17fd7370a4c3b338a74b.gif) |
|---|---|---|---|
| w | w | w | w |
| w | w | f | w |
| w | f | w | w |
| w | f | f | w |
| f | w | w | w |
| f | w | f | w |
| f | f | w | w |
| f | f | f | w |
und bei x Variablen sind es 2x Weltzustände, die nach genau dem Verfahren untersucht werden, das wir im Zusammenhang mit zwei Variablen dokumentiert haben. Die Prüfung der logischen Determiniertheit von Sätzen mit vielen Variablen dauert nur ein wenig länger. Da die Prüfung mechanisch vonstatten gehen kann, darf man sie getrost den Computern überlassen. Nur zum Verständnis des Grundprinzips bedarf es der natürlichen Intelligenz.
Wollen Sie prüfen, warum der obige Schluss aussagenlogisch gültig ist? Es handelt sich um das Transitivitätsgesetz, das auch dem modus barbara zugrunde liegt. Falsch kann der Satz nur sein, wenn das Konsequens falsch und das Antecedens wahr sind. Das Konsequenz ist nur in den Weltzuständen 2 und 4 falsch. In diesen Zuständen ist aber auch der Ausdruck in der eckigen Klammer falsch. Im Weltzustand 2 wegen der zweiten runden Klammer und im Weltzustand 4 wegen der ersten runden Klammer. Mit ein wenig Intelligenz muss man nicht alles durchrechnen.
Prädikaten- oder Quantorenlogik
Um über die Aussagenlogik hinausgehen und durch die innere Struktur der Sätze (über Quantoren und Prädikate) bedingte logische Zusammenhänge aufzeigen zu können, bedarf es der Einführung einiger zusätzlicher Symbole. Es ist dies die Sprache der Prädikatenlogik erster Stufe.
Wir notieren:
a, b, c, ... für Gegenstandskonstante und Eigennamen,
F, G, H, ... für Prädikate,
x, y, z, ... für Gegenstandsvariable,
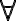 ,
, 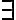 ... für Quantoren, mit denen Gegenstandsvariable gebunden werden können.
... für Quantoren, mit denen Gegenstandsvariable gebunden werden können.
Dabei bezeichnet 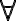 den Allquantor:
den Allquantor:
Für alle x gilt (...)
Es gibt mindestens ein x, für das gilt (...).
Wir ergänzen die Definitionen für die neu hinzugekommenen logischen Zeichen, den Allquantor und den Existenzquantor.
- Ein mit
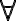 gebildeter Satz ist dann wahr, wenn der dem Quantor folgende Ausdruck auf alle Objekte des vom Quantor gebundenen Variablenbereichs zutrifft (im Beispiel:
gebildeter Satz ist dann wahr, wenn der dem Quantor folgende Ausdruck auf alle Objekte des vom Quantor gebundenen Variablenbereichs zutrifft (im Beispiel: 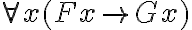 ist genau dann wahr, wenn für alle x gilt: Wenn x die Eigenschaft F hat, dann hat x die Eigenschaft G - kurz: Alle F sind G.
ist genau dann wahr, wenn für alle x gilt: Wenn x die Eigenschaft F hat, dann hat x die Eigenschaft G - kurz: Alle F sind G. - Ein mit
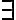 gebildeter Satz ist genau dann wahr, wenn der dem Quantor folgende Ausdruck auf mindestens ein Objekt des vom Quantor gebundenen Variablenbereichs zutrifft (im Beispiel:
gebildeter Satz ist genau dann wahr, wenn der dem Quantor folgende Ausdruck auf mindestens ein Objekt des vom Quantor gebundenen Variablenbereichs zutrifft (im Beispiel: 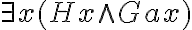 ist genau dann wahr, wenn wenigstens ein Objekt des Diskussionsbereichs von x sowohl die Eigenschaft H hat als auch zum Objekt a in der Relation G steht.
ist genau dann wahr, wenn wenigstens ein Objekt des Diskussionsbereichs von x sowohl die Eigenschaft H hat als auch zum Objekt a in der Relation G steht.
Sie sehen vielleicht schon jetzt, dass die kategorischen Urteile der Syllogistik sich als Sätze der Prädikatenlogik entpuppen, die mit Allquantoren und Existenzquantoren gebildet werden können.
Mit den bekannten Zeichen der Junktorenlogik lassen sich umgangs- und fachsprachliche Sätze beliebiger Komplexität in die Symbolik der Prädikatenlogik übertragen und auf ihre logischen Strukturen und Zusammenhänge überprüfen. Einige (zunächst auf die Übersetzung beschränkte) Beispiele mögen das verdeutlichen:
- Hans (a) ist ein Mörder (F): Fa
- Hans (a) hat Peter (b) geschlagen (G) und Otto (c) beleidigt (H):
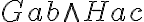
- Alle Mörder (F) sollen bestraft werden (G):
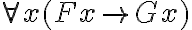 (wörtliche Rückübersetzung: Für alle Dinge dieser Welt gilt, wenn sie Mörder sind, dann sollen sie bestraft werden
(wörtliche Rückübersetzung: Für alle Dinge dieser Welt gilt, wenn sie Mörder sind, dann sollen sie bestraft werden - Einige Schuldner (S) zahlen (Z) nicht:
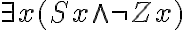 (wörtliche Rückübersetzung: Es gibt mindestens ein Ding, für das gilt: Es ist ein Schuldner, und es zahlt nicht.)
(wörtliche Rückübersetzung: Es gibt mindestens ein Ding, für das gilt: Es ist ein Schuldner, und es zahlt nicht.)
Die Sätze (3) und (1) sind häufig bemühte Ober- und Untersatzbeispiele für den richterlichen Syllogismus im Gewande des modus barbara, mit dem messerscharf auf den Schlusssatz: Hans wird bestraft; Ga geschlossen wird. Können wir das aber wirklich so ohne weiteres? Um den klassischen modus barbara handelt es sich schon deshalb nicht, weil der zweite Satz kein kategorisches Urteil nach der Urteilslehre der Syllogistik ist. Notieren wir die Prämissen:
1. 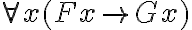 |
(1) |
2. 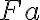 |
(2) |
Ein Übergang zu der Konklusion Ga fällt jedenfalls nicht unmittelbar ins Auge. Dennoch haben wir das Gefühl, dass ein solcher Übergang möglich sein muss. Gefühle mögen täuschen, und die moderne Logik soll sich ja gerade dadurch auszeichnen, dass, nachdem man einige Übergangsregeln akzeptiert hat, die Form allein und kein trügerisches Gefühl über die korrekte Ableitung, die logische Folgerungsbeziehung, entscheidet. Wir benötigen für unsere Zwecke zwei Übergangsregeln. Die erste besagt, dass Zusammenhänge, die von allen Dingen mit einer bestimmten Eigenschaft behauptet werden, auch für ein konkretes Objekt mit eben dieser Eigenschaft gelten (Allbeseitigung - symbolisch: Der Satz 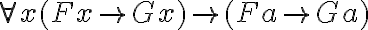 ist logisch wahr. Mit noch anderen Worten: aus
ist logisch wahr. Mit noch anderen Worten: aus 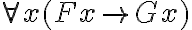 folgt
folgt 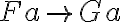 ). Die zweite besagt, dass, wer
). Die zweite besagt, dass, wer 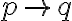 und p annimmt, auch q annehmen muss (modus ponendo ponens - symbolisch: Der Satz
und p annimmt, auch q annehmen muss (modus ponendo ponens - symbolisch: Der Satz ![{[(p}\rightarrow{q)}\wedge{p]}\rightarrow{q} {[(p}\rightarrow{q)}\wedge{p]}\rightarrow{q}](https://moodle.uni-saarland.de/filter/tex/pix.php/aa33347618c7078cdde6e309ed319dcf.gif) ist logisch wahr. Mit anderen Worten: aus
ist logisch wahr. Mit anderen Worten: aus 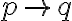 und p folgt q). Mit Hilfe dieser Regeln lässt sich die begonnene Ableitung vervollständigen:
und p folgt q). Mit Hilfe dieser Regeln lässt sich die begonnene Ableitung vervollständigen:
3. 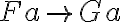 |
Allbeseitigung (1) |
4. 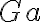 |
modus ponendo ponens (2) (3) |
Prädikatenlogische Folgerungsbeziehungen und Äquivalenzen
Wie für die Aussagenlogik können wir auch für die Prädikatenlogik logisch gültige Schlussformen und Äquivalenzen notieren:
Nun haben wir schon fast alle Voraussetzungen für die Rekonstruktion des richterlichen Urteils im sog. deduktiven Hauptschema zur Hand.
Der Kalkül des natürlichen Schließens
Wenn man das Erlernte praktisch anwenden will, so bietet sich als Darstellungsform der sog. Kalkül des natürlichen Schließens an. In ihm notiert man die Sätze, mit denen man arbeitet, in laufender Nummerierung. Links erscheinen die Ordnungszahlen und rechts die Zahlen der Sätze, aus denen ein Satz seine Begründung erhält. Erscheint links wie rechts dieselbe Zahl, so ist der Satz nicht mit Hilfe der logischen Schlussregeln gefolgert worden. Er dient im Rahmen der geprüften Ableitung als Prämisse (Annahme). Die anderen Sätze sind erschlossen. Und wenn man will, kann man zur Illustration die Schlussregel benennen. Betrachten wir das Skandinavierbeispiel:
Zu den Skandinaviern (K) zählen Finnen (F), Schweden (S) und Norweger (N). Lars (a) ist Skandinavier (K). Dann muss er Schwede (S) sein. Denn er ist weder Finne (F) noch Norweger (N).
Im Kalkül des natürlichen Schließens stellt sich die Argumentation wie folgt dar:
| 1. | 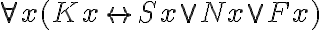 |
(1) Prämisse |
| 2 | 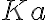 |
(2) Prämisse |
| 3 | 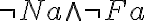 |
(3) Prämisse |
| 4 | 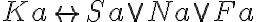 |
(1) prädikatenlogisch |
| 5 | 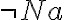 |
(3) aussagenlogisch |
| 6 | 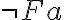 |
(3) aussagenlogisch |
| 7 | 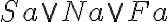 |
(2)(4) aussagenlogisch |
| 8 | 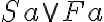 |
(5)(7) aussagenlogisch |
| 9 | 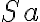 |
(6)(8) aussagenlogisch |
In einer endlichen Anzahl logischer Schritte ist damit für jeden nachprüfbar und übersichtlich die logische Korrektheit der Argumentation dargetan.
Das deduktive Hauptschema
Wir kommen zur Übertragung auf die juristische Fallbehandlung.
Zu begründen ist eine Einzelfallentscheidung. Das Ergebnis der Einzelfallentscheidung kann in einem singulären Satz mit einem deontischen Operator formuliert werden. Der deontische Operator ist neu. Er bringt das Sollen (im Unterschied zum Sein) zum Ausdruck. Als prädikatenlogischen Ausdruck notieren wir für die Einzelfallentscheidung:
Im konkreten Fall (a) ist die Rechtsfolge (R) geboten (O).
Es muss eine deduktiv gültige Argumentation zu der Entscheidung führen. Das bedeutet: Entweder ruht die Einzelfallentscheidung in sich selbst oder aber in den Gründen (Prämissen), die zu ihrer Begründung angeführt werden. Darin muss sich ein Satz mit einem deontischen Operator finden. Sonst könnte kein singulärer Satz mit einem deontischen Operator abgeleitet und das Postulat der deduktiv gültigen Argumentation nicht erfüllt werden.
Wenn wir davon ausgehen, dass juristische Einzelfallentscheidungen nicht in sich selbst ruhen, müssen Gründe angeführt werden, warum die Entscheidung so und nicht anders ausgefallen ist. Wir beginnen mit der Einführung des Sachverhalts. Das ist die Beschreibung eines singulären Geschehens, für die wir als prädikatenlogischen Ausdruck notieren:
Im konkreten Fall (a) haben wir es mit einem Sachverhalt mit den Merkmalen (S) zu tun.
Auch das logisch ungeübte Auge sieht sogleich, dass es von (2) zu (1) keinen deduktiven Übergang gibt. Dazu benötigen wir mindestens noch eine weitere Prämisse. Versuchen wir es zunächst einmal mit der Einführung der Minimalbedingung zur Erfüllung des Deduktivitätspostulats! Das ist ein bedingter singulärer Normsatz, für den wir als prädikatenlogischen Ausdruck notieren:
Wenn der konkrete Fall (a) die Sachverhaltsmerkmale (S) aufweist, dann soll die Rechtsfolge (R) eingreifen.
Mit einem solchen bedingten Normsatz ist das Deduktivitätspostulat erfüllt, weil nun aus (3) und (2) die Einzelfallentscheidung (1) logisch folgt. Logische Bedenken könnten wir gegen eine solche Begründung nicht erheben, wohl aber rechtliche. Das Gleichbehandlungsgebot verlangt die Heranziehung genereller und allgemeiner Normen. Kadijustiz ist nicht erlaubt.
Wir müssen deshalb eine universelle bedingte Norm einführen, für die wir als prädikatenlogischen Ausdruck notieren:
In allen und nur den Fällen (x), in denen die Tatbestandsvoraussetzungen (T) erfüllt sind, soll die Rechtsfolge (R) ausgesprochen werden.
Mit dieser Formulierung treffen wir ganz gut die dem Juristen bekannte Redeweise von der Aufspaltung der Normen in einen Tatbestand (= Voraussetzungsteil) und eine Rechtsfolge. Wir kommen aber in Schwierigkeiten mit der Erfüllung des Deduktivitätspostulats. Es gibt keinen deduktiv gültigen Übergang von (4) und (2) zu (1). Den gäbe es nur, wenn wir beim Sachverhalt Ta statt Sa notiert hätten. Mit Sa aber müssen wir eine logische Kluft zwischen der Sachverhaltsprämisse und der Normprämisse feststellen. Diese kann nur durch die Aufnahme weiterer Prämissen überbrückt werden, welche die Sachverhaltsbeschreibung und den Voraussetzungsteil des Normsatzes miteinander verbinden. Hier handelt es sich regelmäßig um semantische Interpretationen (Auslegungshypothesen) der im Voraussetzungsteil des Normsatzes verwendeten Begriffe mit Richtung auf die zur Beschreibung des individuellen Sachverhalts verwendeten Begriffe. Wegen des Gleichbehandlungsgebots müssen auch diese semantischen Interpretationen allgemein sein. Als Beispiel können wir folgenden prädikatenlogischen Ausdruck für eine semantische Interpretation wählen:
Fälle (x) mit den Merkmalen (S) gehören zu (T).
(5), (4) und (2) erlauben die Folgerung auf (1). Auch (3) ist in (5) und (4) enthalten.