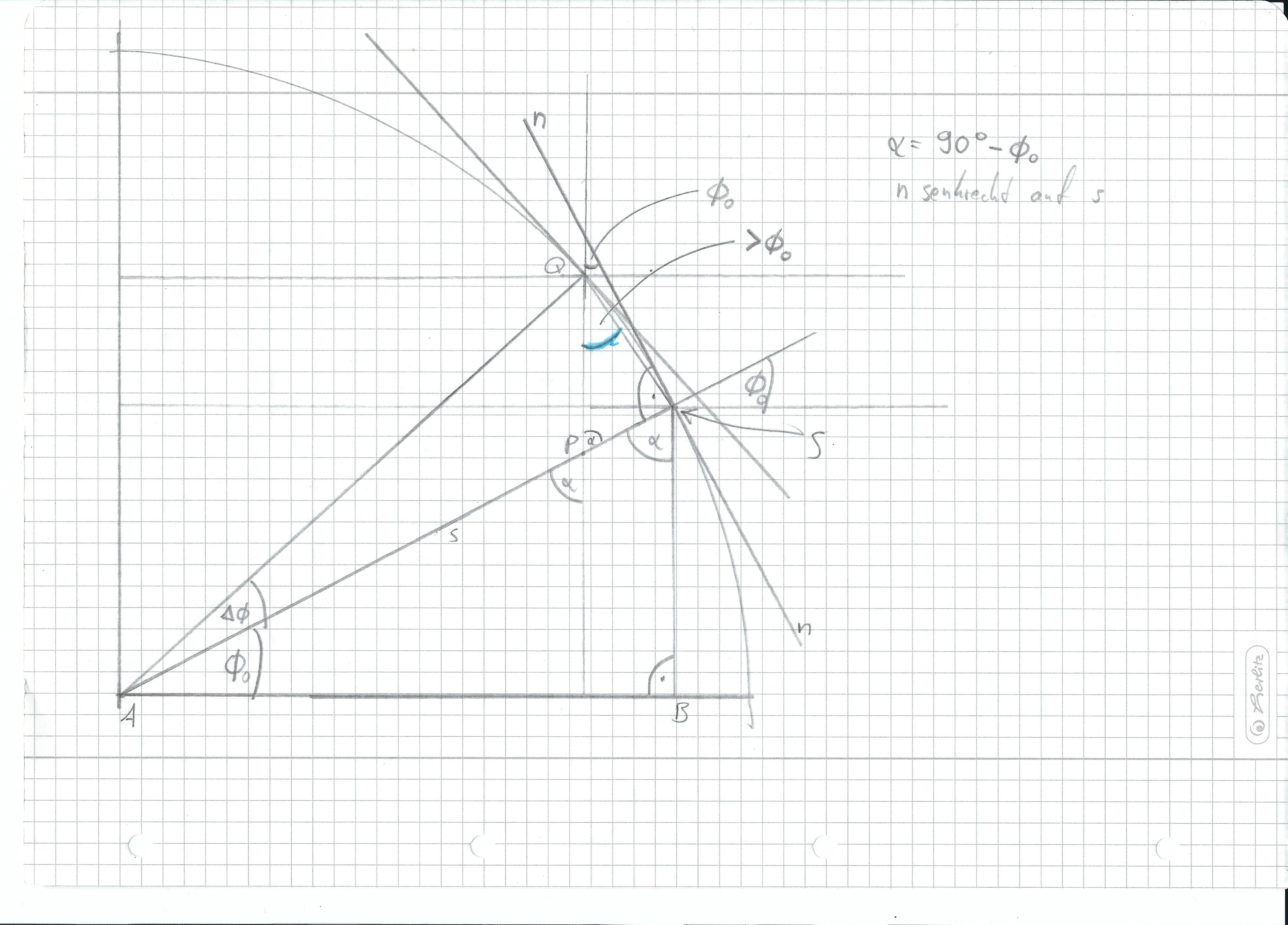
In der Vorlesung hatte ich die geometrische Herleitung der Ableitung des Sinus nicht ganz verstanden. Beim Nachbereiten hab ich mich gefragt: Wieso ist der obere Winkel (im Bild (s. Anhang) blau markiert) in dem kleinen Dreieck, das im "Zoom" an der Tafel gezeichnet war, gleich Phi-0? Wie auf dem Bild zu sehen ist, findet sich der Winkel alpha aus dem Dreieck ABS auch beim Punkt P im Dreieck PSQ. Außerdem sieht man, dass der Winkel, der in diesem Dreieck bei S liegt (also der Winkel QSP), kleiner als 90° sein muss. Denn von dem rechten Winkel fehlt ja ein Stück. (Q liegt ja nicht auf der Tangente n, die am Kreis an S anliegt.) Wenn dieser Winkel aber kleiner als 90° ist, muss der dritte Winkel im Dreieck größer als Phi-0 sein, weil sie ja zusammen 180° ergeben müssen. Also kann dort gar nicht der Phi-0 liegen, sondern nur im Limes. Am Ergebnis ändert das natürlich nichts, die Ableitung bleibt der Kosinus. Vielleicht hilfts ja trotzdem dem einen oder anderen, der die Herleitung auch nicht ganz verstanden hatte.
Anmerkung zur geom. Herleitung der Ableitung des Sinus
von Julian Jakob Schöndorf -
Anzahl Antworten: 2
Als Antwort auf Julian Jakob Schöndorf
Re: Anmerkung zur geom. Herleitung der Ableitung des Sinus
von Philipp Hövel -
Hallo Julian,
vielen Dank für die Frage! Da hast du gut aufgepasst und bist schon auf der richtigen Spur! Hier der Versuch einer Präzisierung:
- Wo phi_0 als Stufen- oder Wechselwinkel auftaucht, ist klar, oder?
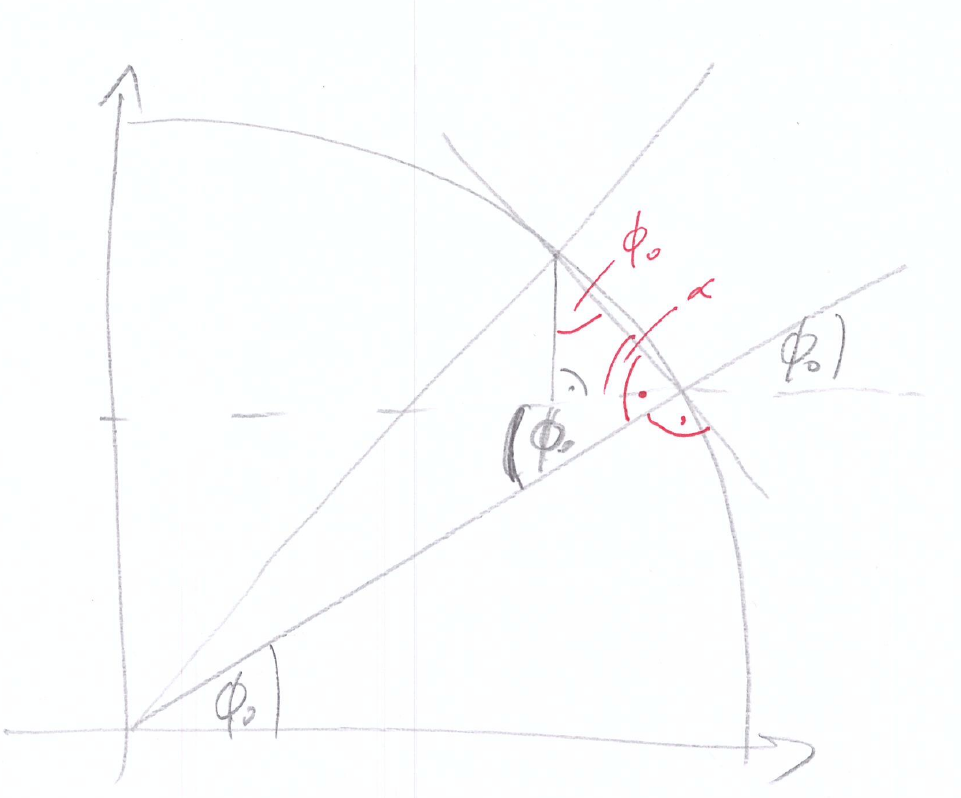
- Die Argumentation, das phi_0 der Spitze des Dreiecks auftaucht (bei dir blau, unten rot), ergibt sich im Grenzfall kleiner Delta phi, also wenn die Gerade durch SQ tangential an den Kreis anliegt. Dann gibt es die roten, rechten Winkel und man kann mit der Winkelsumme des Dreiecks argumentieren. Das reicht uns aber aus, das wir an der Ableitung, also infinitesimale Änderung von phi_0, interessiert sind.
Hilft das weiter?
Viele Grüße
Philipp
Als Antwort auf Philipp Hövel
Re: Anmerkung zur geom. Herleitung der Ableitung des Sinus
von Julian Jakob Schöndorf -
Alles klar, vielen Dank!